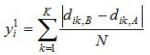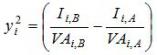Introduzione
Siamo di nuovo alle soglie di una nuova riforma della Pac (di fatto entrerà in vigore nel 2015) e, come già più volte in passato, gli analisti si pongono una questione che ha, allo stesso tempo, interesse puramente scientifico e notevole rilevanza politica: che impatti avrà la riforma sui risultati e le perfomance delle imprese agricole e, quindi, dell’agricoltura dell’UE e di suoi territori? La risposta a questa domanda, in realtà, rimanda ad un'altra e più profonda questione: come risponderanno le imprese agricole alla riforma?
L’obiettivo di questo breve articolo è discutere intorno a quest’ultima questione con particolare riferimento a quale strumentazione e, prima ancora, a quale approccio logico e metodologico è possibile mettere in campo per provare a fornire una risposta convincente a tali domande di ricerca nonché di valutazione delle politiche. Per meglio mettere in luce le implicazioni metodologiche che si vogliono qui evidenziare, verranno fornite alcune evidenze empiriche riferite non all’attuale riforma (per la quale, evidentemente, non è possibile produrre alcuna verifica ex post degli impatti) bensì alla riforma della Pac del 2003, la cosiddetta Riforma Fischler, che ha rivoluzionato i pagamenti del primo pilastro della Pac imponendo (sebbene in modalità e tempi diversi) il disaccoppiamento totale e che, quindi, per contenuti e portata ha sollevato un vivace dibattito proprio circa i suoi effetti attesi (Sorrentino et al., 2011).
L’approccio metodologico qui seguito per stimare tale risposta alla precedente riforma della Pac è quello degli effetti di trattamento a valori multipli (continui o discreti) (Hirano e Imbrens, 2004; Imbens e Wooldridge, 2009; Esposti, 2014). Tale approccio è applicato ad un panel bilanciato di imprese agricole italiane incluse nel campione Rica e osservate nel periodo 2003-2007, cioè nel periodo immediatamente precedente e immediatamente successivo alla riforma in questione che, almeno in Italia, è stata implementata a partire dal 2005. Non si vuole qui entrare nel merito delle difficoltà connesse all’applicazione di questi approcci econometrici alla riforma del primo pilastro della Pac. Per approfondimenti su questo si rimanda a Esposti (2011; 2014). L’obiettivo è piuttosto mostrare come tale approccio permetta di mettere in luce la natura e l’entità della risposta delle imprese alla riforma della Pac (il disaccoppiamento, in questo caso) senza dover formulare controverse ipotesi e specificare complessi modelli teorici relativi al comportamento delle imprese stesse.
La risposta al disaccoppiamento: le ipotesi teoriche
La letteratura concernente la risposta delle imprese agricole al disaccoppiamento del sostegno è ampia e articolata (Sckokai, 2005; Serra et al., 2009; Moro e Sckokai, 2011). Proviamo qui a sintetizzare le principali argomentazioni teoriche che tale letteratura evoca per motivare direzione ed entità di questa risposta.
In uno schema teorico di stampo neoclassico, la risposta al disaccoppiamento totale è del tutto analoga alla risposta ad un cambiamento dei prezzi relativi (o dei valori marginali) dei prodotti effettivamente o potenzialmente realizzati dall’impresa. Allo stesso modo, quindi, l’entità della risposta al disaccoppiamento dipende dall’elasticità dell’offerta rispetto a tali valori che, a sua volta, è espressione della tecnologia di produzione multi-prodotto; in ultima istanza, dal grado di sostituibilità di input e output. Ne consegue che la riforma della Pac del 2003 può certamente avere sortito un effetto in termini di composizione del prodotto, ma l’entità di questo effetto dipende dalla tecnologia di produzione e, allo stesso tempo, dall’autonoma dinamica dei prezzi di mercato tra i due periodi in considerazione (prima e dopo la riforma) che può avere mitigato o amplificato, secondo la direzione di movimento, questa stessa risposta al disaccoppiamento.
Come ampiamente discusso in questa letteratura, tuttavia, vi sono altri fattori oltre a tecnologia e prezzi che determinano la risposta al disaccoppiamento. In particolare, la presenza di incertezza mette in gioco altre due caratteristiche soggettive dell’imprenditore agricolo: l’attitudine verso il rischio e le aspettative (relative sia a prezzo che a perfomance produttive). Questi aspetti inducono altri due effetti che incidono nella risposta al disaccoppiamento, quelli che Hennessy (1998) indica come effetto ricchezza e effetto sicurezza. Inoltre, una caratteristica tipica della produzione agricola consiste nella presenza di fattori della produzione (e, di conseguenza, di output) che implicano significativi costi di aggiustamento. Di conseguenza, la riposta immediata (o di breve periodo) può essere fortemente limitata da queste rigidità (aggiustamento parziale) mentre, al contrario, allorché questi vincoli vengono meno (cioè, per definizione, nel lungo periodo) la risposta al disaccoppiamento può essere completa (aggiustamento pieno) benché comunque condizionata dall’entità di questi costi di aggiustamento. Peraltro, l’entità di tale aggiustamento pieno, oltre che dai relativi costi, può essere condizionato anche dalla presenza di mercati imperfetti e, in particolare, da restrizioni nel mercato del credito. In tale circostanza, il disaccoppiamento determina un aumento di risorse finanziarie liberamente disponibili che non sarebbero state ottenute, se non a costi elevati, ricorrendo al credito e ciò rende possibili le scelte di investimento.
Qui si vuole riassumere le conclusioni e le implicazioni di questa letteratura teorica ed empirica con riferimento al tema qui di interesse, cioè se e quanto le imprese rispondono all’entità del disaccoppiamento del sostegno, ovvero all’intensità del trattamento. Per entità del disaccoppiamento qui si intende quanto grande, in relazione alla dimensione di impresa, è il sostegno che passa dall’essere associato a specifiche produzioni (accoppiato) all’essere erogato senza condizionamenti produttivi (disaccoppiato). Una prima implicazione consiste nel fatto che, come già messo in evidenza, tale risposta assume due diverse forme e intensità a seconda che si consideri la risposta di breve o di lungo periodo.
Nel breve periodo, la risposta consiste essenzialmente nel modificare l’allocazione di quei fattori della produzione che possono essere effettivamente riallocati nel breve periodo tra le varie produzioni che possono essere attivate nel breve termine. Nel lungo periodo, invece, la risposta prende la forma di investimenti che mobilizzano quei fattori e quelle produzioni che sono in realtà fissi nel breve periodo. Quindi, quantificare l’entità della risposta richiede necessariamente l’adozione di due diversi tipi di indicatori o variabili. In secondo luogo, la variazione dell’entità della risposta in seguito alla variazione dell’intensità del disaccoppiamento (trattamento) risulta sostanzialmente differenziata nel breve e nel lungo periodo. Da un lato, possiamo facilmente arguire che nel breve periodo la risposta cresce al crescere dell’entità del trattamento. Maggiore disaccoppiamento, quindi maggiore ammontare dei pagamenti che da accoppiati divengono disaccoppiati, implica una maggiore variazione dei valori marginali tra le attività produttive. Possiamo in astratto assumere che tanto più un’impresa riceve sostegno dal primo pilastro della Pac (in termini relativi, come verrà chiarito in seguito), tanto più grande sarà la quota di fattori della produzione (lavoro e terra, in particolare) dedicata alle produzioni fortemente sostenute ai tempi del sostegno accoppiato e, quindi, libere di essere riallocate in seguito al disaccoppiamento.
Tuttavia, benché monotonicamente crescente, sembra plausibile assumere che tale risposta sia concava (risposta concava, Figura 1a), o non-convessa, esattamente come lo sarebbe la risposta alla variazione di prezzi relativi (Chambers, 1988). Ci sono tre fattori che possono spiegare tale risposta concava. In primo luogo, la variabile che misura la risposta di breve periodo può avere, come nel presente caso, un limite superiore. Pertanto, allorché questo massimo viene raggiunto o ci si avvicina a esso, un ulteriore aumento dell’intensità del trattamento indurrà una minima o nulla ulteriore risposta. Generalizzando, possiamo concludere che più l’aggiustamento è vicino a questo limite superiore minore sarà la risposta marginale.
Figura 1 - Risposta di breve (a) e di lungo (b) periodo al disaccoppiamento con intensità crescente del trattamento
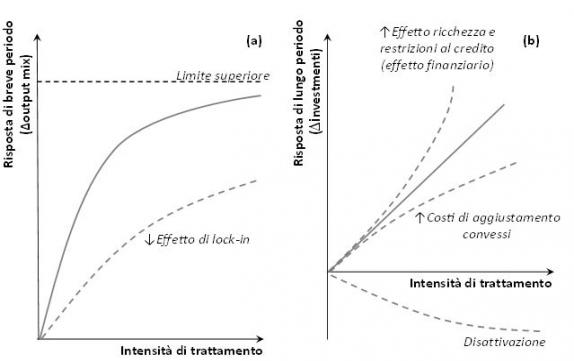
Fonte: Elaborazione da Esposti (2014)
In secondo luogo, la risposta di breve periodo per definizione incontra le rigidità associate ai fattori e alle produzioni quasi-fisse; rigidità che in pratica prende la forma di costi di aggiustamento particolarmente elevati. Quindi, l’aggiustamento delle imprese agricole riguarderà in prima battuta quelle attività produttive che non implicano elevati costi di aggiustamento. Ulteriore aggiustamento indotto da una crescita dell’intensità del disaccoppiamento incontrerà costi crescenti e questo si rifletterà in una risposta decrescente alla crescita marginale di questa intensità
Il terzo è ultimo fattore risiede nel fatto che, in effetti, il sostegno accoppiato non è proporzionale alle risorse (lavoro, terra, ecc.) dedicate alle produzioni sostenute semplicemente perché, storicamente, la Pac ha sostenuto più alcune produzioni di altre. Ma questa motivazione può in realtà determinare una risposta in senso opposto rispetto alle due precedenti. Si può infatti argomentare che le attività maggiormente sostenute sono quelle che più rapidamente vengono disattivate in seguito al disaccoppiamento dal momento che l’adozione di quelle meno o per nulla sostenute era già evidentemente guidata dai prezzi di mercato. In altre parole, i produttori che compiono scelte ottimizzanti sono già più vicini all’efficienza allocativa allorché realizzano produzioni poco o per nulla sostenute, quindi quando sono interessati da una minore entità del trattamento. Pertanto, per questi, il disaccoppiamento può comportare un aggiustamento più contenuto rispetto ai produttori che ricevono più pagamenti. Se ciò non accade, l’interpretazione è che tali produttori che realizzano le produzioni maggiormente sostenute sono evidentemente bloccati in queste scelte produttive (effetto di lock-in). Quest’ultimo effetto può controbilanciare le altre due forze che inducono una risposta concava e ciò sarà tanto più vero quanto minore è questo effetto di lock-in (Figura 1a).
Spostando l’attenzione dal contesto di breve periodo a quello di lungo, la natura e la forma della risposta al disaccoppiamento cambiano notevolmente. La principale differenza risiede nel fatto che in un orizzonte temporale ampio la risposta delle imprese agricole prende prevalentemente la forma dell’investimento (o del disinvestimento). Diversi precedenti lavori hanno già teorizzato come l’effetto atteso del disaccoppiamento sia un aumento della propensione all’investimento, cioè della domanda di beni di investimento. Se questo aumento risulti costante (risposta lineare), crescente (risposta monotona convessa) o decrescente (risposta monotona concava) dipende dall’effetto combinato di forze contrastanti. La suddetta letteratura mette in evidenza come l’effetto ricchezza, se si assume una avversione al rischio decrescente (Decreasing Absolute Risk Aversion) e in condizioni di significative restrizioni nel mercato creditizio, può determinare una risposta convessa1. Al contrario, costi di aggiustamento convessi (cioè, costi di aggiustamento crescenti con il crescere del livello di investimento) possono determinare una risposta concava. Quindi, le tre forme di risposta mostrate nella figura 1a sono tutte teoricamente possibili, dal momento che tutte queste forze coesistono e ciò che effettivamente osserviamo dipende da quale di queste realmente prevale. In particolare, se l’effetto ricchezza e le restrizioni creditizie prevalgono (in questo caso parliamo di effetto finanziario) osserveremo una forma convessa della risposta. Possiamo anche ipotizzare, infine, che il disaccoppiamento totale induca, invece, alcune imprese semplicemente a disattivare parte delle loro attività o persino uscire dal settore. In tal caso, dovremmo piuttosto osservare una risposta che prende la forma di una riduzione convessa della domanda di investimento. Tuttavia, questa disattivazione (o uscita) è limitata dai vincoli imposti dalla stessa riforma della Pac (in particolare, l’eco-condizionalità) e riguarda prevalentemente le attività agricole non professionali, condotte spesso da agricoltori anziani o con una prevalente attività extra-agricola. Queste unità produttive agricole sono poco o per nulla rappresentate nel campione di aziende qui considerato, cioè il panel bilanciato delle imprese Rica in Italia, che per costruzione esclude le attività cessate e quelle non professionali. Ciò nondimeno, l’approccio metodologico qui adottato non esclude una risposta negativa all’intensità del disaccoppiamento in termini di domanda di investimento. Una tale evidenza empirica, in effetti, andrebbe interpretata proprio come la prevalenza di una risposta di disattivazione da parte delle imprese agricole.
In termini più generali, il presente articolo vuole verificare se queste ipotesi relative alla risposta al disaccoppiamento sono effettivamente supportate dai dati e che tipo di risposta risulta alla fine prevalente. A differenza di precedenti contributi empirici in quest’ambito, tuttavia, la metodologia qui proposta non dipende dalla specificazione o da assunzioni restrittive ex ante circa i fattori fondamentali sottostanti: tecnologia produttiva, attitudine soggettiva al rischio, formazione delle aspettative, costi di aggiustamento. Tutte queste assunzioni e specificazioni necessarie nell’approccio convenzionale, non solo lo rendono di complessa applicazione pratica, se non impraticabile, ma richiedono anche cautela nell’interpretazione dei risultati (Moro e Sckokai, 2011).
Al contrario, il maggiore vantaggio e la novità dell’approccio qui adottato risiedono nel fatto che la verifica empirica dell’impatto del disaccoppiamento è conseguita direttamente seguendo la logica degli effetti di trattamento a valori multipli che non richiede particolari assunzioni sui suddetti aspetti. La teoria continua ad essere necessaria al fine di formulare alcune plausibili ipotesi circa la relazione funzionale tra queste variabili e l’intensità del trattamento. Tale relazione può assumere diverse forme e, di conseguenza, la specificazione adottata, e da stimare, dovrebbe risultare sufficientemente flessibile per ammetterle tutte (Figura 1a). I risultati ottenuti, poi, possono rivelare quale di queste forme risulta empiricamente validata e, quindi, l’effettiva natura e rilevanza delle caratteristiche e dei fattori sottostanti.
La risposta al disaccoppiamento: verifica empirica secondo la funzione dose-risposta
Si consideri un campione di N imprese agricole. Per ogni generica i-esima unità del campione, i = 1,…, N, osserviamo un insieme di covariate Xi, il livello di trattamento Ti , la variabile risultato del trattamento Yi . Si definisca, "![]() i, un insieme di esiti potenziali del trattamento
i, un insieme di esiti potenziali del trattamento ![]() , dove
, dove ![]() è l’insieme dei potenziali livelli di trattamento e
è l’insieme dei potenziali livelli di trattamento e ![]() è una variabile casuale che, per ogni i-iesima unità, associa un particolare trattamento T ad un esito potenziale Yi . Evidentemente, di questi esiti potenziali, solo uno è effettivamente osservato, quello associato al trattamento realmente ricevuto Ti. Hirano e Imbens (2004) definiscono
è una variabile casuale che, per ogni i-iesima unità, associa un particolare trattamento T ad un esito potenziale Yi . Evidentemente, di questi esiti potenziali, solo uno è effettivamente osservato, quello associato al trattamento realmente ricevuto Ti. Hirano e Imbens (2004) definiscono ![]() funzione dose-risposta individuale. In realtà, qui interessa piuttosto la funzione dose-risposta media o attesa (o average Dose-Response Function, aDrf),
funzione dose-risposta individuale. In realtà, qui interessa piuttosto la funzione dose-risposta media o attesa (o average Dose-Response Function, aDrf), ![]() . Questa è, nel presente caso, l’espressione empirica delle funzioni teoriche rappresentate in figura 1.
. Questa è, nel presente caso, l’espressione empirica delle funzioni teoriche rappresentate in figura 1.
L’approccio che segue questa intuizione è stato originariamente proposto da Hirano e Imbens (2004) ed è basato sul concetto di Generalized Propensity Score (GPS), a sua volta generalizzazione al caso dei trattamenti a valori multipli (continui o discreti) del Propensity Score Matching largamente usato per i trattamenti binari (Esposti, 2014). L’approccio di Hirano-Imbens prevede diversi passaggi di stima parametrica. Il primo consiste nella stima delle GPSi, cioè della probabilità r che all’i-esima unità venga assegnata l’intensità di trattamento T date le sue caratteristiche osservabili Xi: ![]() . L’ultimo passaggio consiste, data la stima GPSi, nella stima dell’
. L’ultimo passaggio consiste, data la stima GPSi, nella stima dell’ ![]() ,
, ![]() , cioè del valore atteso della funzione dose-risposta per ogni diverso livello dell’intensità di trattamento2.
, cioè del valore atteso della funzione dose-risposta per ogni diverso livello dell’intensità di trattamento2.
Nel presente caso, il trattamento è proprio la riforma della Pac del 2003 (applicata a partire dal 2005 in Italia), cioè il cambiamento del sostegno erogato dal primo pilastro da una forma accoppiata alle singole attività produttive ad una forma totalmente disaccoppiata. Evidentemente, la partecipazione al trattamento non è volontaria giacché le imprese agricole non possono scegliere di rimanere nel vecchio regime. D’altro canto, si osserva effettivamente un numero limitato di imprese che risultano non trattate ma semplicemente perché queste non hanno ricevuto aiuti accoppiati nel triennio di riferimento (2000-2002) e, di conseguenza, non hanno acquisito diritto al pagamento disaccoppiato, il Pua. Proprio per questo si tratta di imprese del tutto particolari che possono con difficoltà essere considerate valide osservazioni controfattuali (Esposti, 2014).
Peraltro, la verifica empirica della risposta al trattamento può basarsi anche solo sulle imprese trattate cioè quelle che a partire dal 2005 hanno visto il sostegno trasformarsi in Pua. Tra queste imprese trattate, l’intensità del trattamento è molto diversificato. Ci sono imprese fortemente dipendenti dal sostegno del primo pilastro e che, di conseguenza, ne condizionava fortemente le scelte ai tempi del sostegno accoppiato, e altre unità produttive in cui il sostegno, e relativo condizionamento, risulta sostanzialmente marginale. È evidente che la risposta al disaccoppiamento sarà più forte nel primo caso, meno nel secondo. Il contesto, quindi, appare ideale per l’applicazione di una approccio con effetti di trattamento a valori multipli.
L’intensità del trattamento (TI) esprime l’ammontare del sostegno ricevuto ma, evidentemente, questo dipende anche dalla dimensione d’impresa. Perciò, per esprimere una TI che colga davvero la rilevanza del sostegno Pac sull’attività dell’impresa agricola, TI viene qui espresso come il rapporto tra il sostegno ricevuto dal primo pilastro della Pac (accoppiato prima e poi come Pua) e la Plv aziendale. Per entrambi i valori che entrano nel calcolo della TI viene considerato il valore medio del periodo 2003-2007.
Più che nella definizione di una variabile di trattamento con valori multipli, la difficoltà principale nell’applicare l’approccio sopra delineato alla riforma del primo pilastro della Pac del 2003 sta nelle scelta della variabile di risultato del trattamento. Come già accennato e, soprattutto, come chiaramente enfatizzato dalla stessa Commissione Europea (European Commission, 2011; Oecd; 2011), l’obiettivo di tale riforma era il riorientamento al mercato delle imprese agricole europee. Quindi, la risposta al trattamento va rappresentata con una variabile che colga tale riorientamento. Secondo quanto discusso, però, una tale variabile assume diversa natura a seconda se ci muoviamo nel breve e nel lungo periodo. Nel primo caso, una appropriata variabile di risultato (o risposta) al trattamento dovrebbe esprimere il grado di cambiamento del mix produttivo da parte dell’unità produttiva. Quest’ultima, tipicamente, mostra orientamenti produttivi multi-output e, quindi, tale risposta si esprime come un vettore più che come uno scalare. Per ogni elemento di questo vettore, si ha una risposta in termini di orientamento al mercato se si osserva una variazione tra il pre e il post-trattamento. Tale variazione consiste nell’attivazione di una produzione precedentemente non presente nel mix produttivo (o annullamento di una produzione precedentemente realizzata). Peraltro, sebbene la risposta si esprima in un vettore, la variabile risposta Yi deve evidentemente essere uno scalare.
Di conseguenza, la risposta di breve periodo al trattamento viene qui espressa mediante questa variabile:
dove k=1,….,K indica il generico k-esimo prodotto all’interno del vettore delle produzioni potenzialmente attivabili, mentre dik è una variabile dicotomica che assume valore 1(0) se il k-esimo prodotto è (non è) realizzato dall’i-esima unità. A e B esprimono i due momenti nel tempo in cui queste attività vengono osservate. Quindi, A identifica un anno precedente al trattamento (riforma), B indica un anno successivo al trattamento. In sostanza, ![]() è una variante di un semplice indice di similarità tra i due vettori di produzione (in A e in B). Giacché dik è una variabile dicotomica, per costruzione
è una variante di un semplice indice di similarità tra i due vettori di produzione (in A e in B). Giacché dik è una variabile dicotomica, per costruzione ![]() varia tra 0 e 1, dove i valori più vicini allo 0 sono riscontrati nelle imprese agricole il cui vettore espressione dell’output mix rimane sostanzialmente invariato dopo la riforma, quindi imprese che mostrano una risposta debole, mentre i valori più vicini a 1 sono osservati in quelle unità produttive che rispondono alla riforma in modo deciso come risulta da un notevole cambiamento nell’output mix.
varia tra 0 e 1, dove i valori più vicini allo 0 sono riscontrati nelle imprese agricole il cui vettore espressione dell’output mix rimane sostanzialmente invariato dopo la riforma, quindi imprese che mostrano una risposta debole, mentre i valori più vicini a 1 sono osservati in quelle unità produttive che rispondono alla riforma in modo deciso come risulta da un notevole cambiamento nell’output mix.
La scelta di una appropriata variabile di risultato nel caso della risposta di lungo periodo al trattamento/riforma appare, in effetti, più immediato. Come discusso, tale risposta si concretizza in scelte di investimento (o disinvestimento) e, pertanto, la variabile di risultato che esprime tale scelta consiste semplicemente nella variazione della domanda/spesa di investimento dell’i-esima impresa (![]() ) tra l’anno A e l’anno B. Evidentemente, al fine di avere anche in questo caso una variabile non dipendente dalla dimensione di impresa, la spesa di investimento va espressa in relazione alla capacità dell’impresa stessa di sostenerlo. Quindi, la seconda variabile risultato/risposta qui adottata viene così definita:
) tra l’anno A e l’anno B. Evidentemente, al fine di avere anche in questo caso una variabile non dipendente dalla dimensione di impresa, la spesa di investimento va espressa in relazione alla capacità dell’impresa stessa di sostenerlo. Quindi, la seconda variabile risultato/risposta qui adottata viene così definita:
dove VAi esprime il valore aggiunto dell’i-esima unità produttiva.
Un’ultima questione da affrontare per poter applicare l’approccio Hirano-Imbens alla riforma del primo pilastro della Pac, riguarda la scelta degli anni di riferimento A (pre) e B (post-trattamento). Nel presente articolo si considera il campione costante Rica osservato negli anni 2003-2007. Tra le altre motivazioni (Esposti, 2014), tale scelta è dovuta al fatto che si tratta di un periodo che ammette due anni prima e dopo la riforma (2003 e 2007, rispettivamente), simmetrici rispetto al trattamento e sufficientemente lontani da poter scongiurare l’uno effetti anticipati (i contenuti della riforma erano infatti già noti nel 2003 e, pertanto, già anticipabili nel 2004), l’altro i fisiologici tempi di un adeguamento tardivo a livello aziendale (si pensi solo ai vincoli imposti dalle rotazioni culturali). Allo stesso tempo, 2003 e 2007 sono anche sufficientemente vicini al 2005 da escludere (o ridurre al minimo) il rischio di una sovrapposizione con gli effetti di altre riforme (Agenda 2000 prima del 2003; Health Check dopo il 2007). Pertanto, nell’applicazione presentata nel paragrafo successivo sarà: A=2003 and B=2007.3
L’applicazione alla riforma della Pac 2003 in Italia
Il campione costante delle aziende Rica 2003-2007, composto da 6542 unità, consente una valida applicazione dell’approccio Hirano-Imbens alla riforma Fischler del primo pilastro della Pac. Il campione Rica italiano, infatti, contiene tutte le informazioni necessarie non solo rispetto alle variabili di trattamento e risultato per entrambi gli anni di riferimento A e B, ma anche rispetto all’insieme di covariate X che sembra opportuno considerare. Si tratta di quelle variabili che possono allo stesso tempo condizionare sia il livello di trattamento ricevuto da un’unità sia la sua risposta. In particolare, è stata qui considerata una batteria di 10 variabili espressione di tre diverse categorie di fattori (Esposti, 2014): le caratteristiche individuali dell’impresa e dell’imprenditore; la dimensione aziendale; l’orientamento produttivo.
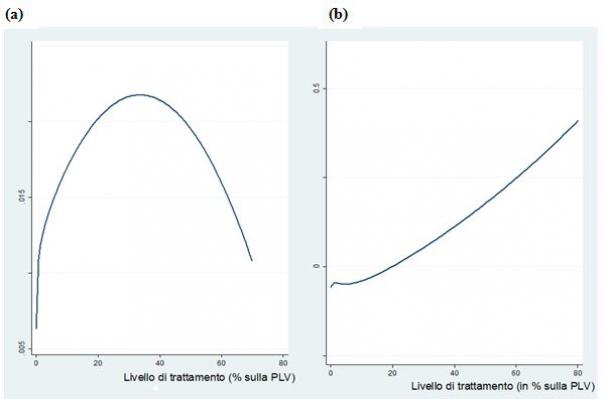
Figura 2 - Stima della funzione dose-risposta attesa (media) per le variabili-risultato y1 (a) and y2 (b)
Fonte: Elaborazione da Esposti (2014)
La figura 2 mostra la stima delle funzioni di dose-risposta per le due variabili considerate e stimate mediante l’approccio parametrico di Hirano-Imbens. Tralasciando i seppur importanti dettagli econometrici (per i quali si rimanda a Esposti, 2014), interessa qui mostrare come, da un lato, il metodo è in grado di riprodurre un tipo di risposta al disaccoppiamento analogo a quello derivante dalle considerazioni teoriche (Figura 1a,b) senza, però, dipendere da alcuna assunzione o specificazione espressione di quei modelli teorici. D’altro canto, e soprattutto, si vuole qui evidenziare come il metodo metta in luce quali, delle possibili relazioni funzionali tra entità della risposta e intensità del trattamento, riescono meglio a cogliere i dati effettivamente osservati, pertanto il reale comportamento delle imprese agricole.
In primo luogo, si noti che la stima della funzione di dose-risposta nel caso del breve periodo mostri la risposta cresce con il crescere dell’intensità del trattamento e raggiunge il suo massimo quando TI = 30%, cioè ben oltre l’intensità di trattamento media nel campione che è di circa il 10%. Oltre questo livello massimo, la risposta comincia a diminuire e a perdere significatività statistica. Siamo in un territorio che riguarda un numero relativamente contenuto di imprese che sono fortemente dipendenti, come peso sulla Plv, dai contributi del primo pilastro della Pac. Rimane il fatto che, se confrontato con quanto previsto dalla teoria (Figura 1a), l’interpretazione di questo risultato riveste un certo interesse.
La risposta è in effetti concava come atteso. Tuttavia dovrebbe essere monotona mentre ciò non si verifica quando si arriva a livelli di sostegno molto elevato. In queste realtà produttive, evidentemente, il livello del sostegno condiziona talmente le scelte produttive da compromettere la capacità di perseguire efficienza allocativa. Ciò sembra spiegabile con un forte effetto di lock-in che subentra in particolare in corrispondenza di questi elevati livelli di sostegno.
I risultati relativi alla seconda variabile di risultato/risposta e concernente la risposta di lungo periodo, y2, risultano (vedi Esposti, 2014) statisticamente meno robusti, fatto facilmente motivabile con la maggiore eterogeneità della risposta delle imprese al trattamento, ma altrettanto interessanti come interpretazione economica. La risposta stimata risulta essere crescente e convessa e, secondo quanto derivante dall’analisi teorica (Figura 1b), ciò sembra escludere un prevalente effetto di disattivazione mentre risulta coerente con la prevalenza di un effetto ricchezza e di significative limitazioni del credito (ciò che abbiamo qui chiamato effetto finanziario). In pratica, la risposta in termini di domanda di investimento sarebbe guidata dal fatto che il disaccoppiamento mette a disposizione delle risorse finanziarie libere che le imprese decidono di investire proprio all’interno dell’attività agricola. E ciò è tanto più vero quanto maggiore è l‘incidenza del sostegno sulla Plv. È come se una maggiore intensità del sostegno disaccoppiato generasse un extra-incentivo all’investimento.
Al di là dei risultati specifici e della loro interpretazione che certamente richiederebbero maggiori approfondimenti, si vuole qui sottolineare come l’approccio qui seguito, e basato sull’econometria degli effetti di trattamento a valori multipli, non solo sembra potersi utilmente applicare all’analisi dell’impatto della riforma del primo pilastro della Pac, ma risulta anche essere particolarmente utile in questo contesto giacché non richiede l’elaborazione e la specificazione di complessi modelli teorici sottostanti. Il metodo è relativamente a-teorico giacché la stima delle funzioni dose-risposta e dei conseguenti effetti di trattamento è interamente guidata dai dati. Ciò non pone tale approccio in alternativa ai modelli teorici. Infatti, la teoria risulta comunque essenziale per una adeguata definizione delle variabili di trattamento e risultato. Ma, soprattutto, questi approcci esclusivamente basati sui dati sembrano utili proprio come complemento all’analisi teorica poiché consentono di verificare quali delle possibili ipotesi teoriche prevale nell’analisi empirica realizzata senza che queste ipotesi teoriche ne condizionino, o persino determinino, gli esiti.
Tale combinazione di analisi e interpretazione teorica con questi approcci data driven sembra quindi particolarmente utile, e persino necessaria, per una valutazione delle politiche che sia più strettamente basata sull’evidenza empirica.
Riferimenti bibliografici
-
Cagliero R., Cisilino F. and Scardera A. (2010), L’utilizzo della Rica per la valutazione di programmi di sviluppo rurale. Roma: Rete Rurale Nazionale
-
Esposti R. (2011), La chiave e la luce: perché valutare la riforma del primo pilastro della Pac è difficile. Are – AgriRegioniEuropa, 7 (25), 9-13
-
Esposti R. (2014), To match, not to match, how to match: Estimating the farm-level impact of the Cap-first pillar reform (or: How to Apply Treatment-Effect Econometrics when the Real World is a Mess). Quaderno di Ricerca n. 403, Dipartimento di Scienze Economiche e Sociali, Università Politecnica delle Marche
-
European Commission (2011), The Cap in perspective: from market intervention to policy innovation. Agricultural Policy Perspectives Briefs, Brief nº 1, European Commission, Directorate-General for Agriculture and Rural Development, Brussels
-
Hennessy D. A. (1998), The Production Effects of Agricultural Income Support Polices Under Uncertainty. American Journal of Agricultural Economics 80: 46-57
-
Hirano K., Imbens G.W. (2004), The propensity score with continuous treatment. In: Gelman, A., Meng, X.L. (eds.) Applied Bayesian Modeling and Causal Inference from Incomplete-Data Perspectives. West Sussex: Wiley InterScience, 73-84
-
Imbens G.W. and Wooldridge J.M. (2009), Recent Developments in the Econometrics of Program Evaluation. Journal of Economic Literature, 47 (1), 5–86
-
Moro D., Sckokai P. (2011), The impact of pillar I support on farm choices: conceptual and methodological challenges. Paper presented at the 122nd Eaae Seminar “Evidence-Based Agricultural and Rural Policy Making: Methodological and Empirical Challenges of Policy Evaluation”, Ancona (Italy), February 17-18
-
Oecd (2011), Evaluation of Agricultural Policy Reforms in the European Union. Paris: Oecd Publishing
-
Sckokai P. (2005), Modelling the impact of agricultural policies on farm investments under uncertainty: the case of the Cap arable crop regime. Working Paper Agr/CA/Apm(2005)13/Final. Paris: Oecd
-
Serra T., Stefanou S., Gil J. M., Featherstone A. (2009), Investment Rigidity and Policy Measures. European Review of Agricultural Economics 36: 103–120
-
Sorrentino S., Henke R., Severini S. (eds.) (2011), The Common Agricultural Policy after the Fischler Reform. National Implementations, Impact Assessment and the Agenda for Future Reforms, Farnham: Ashgate
- 1. In linea di principio, queste forze possono avere un impatto anche sulle scelte di breve periodo, ma condizionano prevalentemente quelle di lungo, cioè la domanda di investimento.
- 2. Per i dettagli econometrici nonché per possibili soluzioni di stima alternative si veda Esposti (2014).
- 3. Si veda Esposti (2014) per una discussione più approfondita sulla scelta degli anni di riferimento A e B.