Introduzione
L’utilizzo di modelli econometrici per la valutazione degli effetti delle politiche e per l’analisi del settore agricolo è una pratica comune nell’analisi empirica; attraverso la specificazione di un modello di comportamento per l’agricoltore in un contesto di tipo competitivo, il modello viene stimato utilizzando diverse metodologie a partire dai dati disponibili. Gli strumenti delle politiche agricole e altre variabili di interesse possono esservi inseriti e allo stesso modo, seppur con opportuni accorgimenti, i risultati empirici possono essere utilizzati ed estesi a modelli di simulazione di politiche alternative e/o costituire un importante input nella costruzione e nella calibrazione di modelli strutturali di mercato.
Nell’analisi econometrica del settore agricolo vengono seguiti sostanzialmente due approcci: un primo approccio, classico, è l’approccio cosiddetto “primale”, che consiste nello specificare ‘direttamente’ il problema di massimizzazione dell’agricoltore, e dunque una funzione di produzione che riassume tutte le caratteristiche tecnologiche; un secondo approccio, più recente, che invece considera il problema “duale”, e dunque arriva ‘indirettamente’ alla specificazione di equazioni comportamentali per il produttore (offerta dei prodotti e domanda/allocazione di input variabili e/o fissi) partendo da funzioni di profitto e/o di costo e/o di ricavo. In considerazione delle oggettive difficoltà di specificazione di una funzione di produzione, specie nel caso di analisi multi-prodotto, l’approccio duale ha avuto un notevole impulso negli ultimi decenni, grazie anche allo sviluppo delle cosiddette “forme funzionali flessibili” che hanno consentito la specificazione di modelli caratterizzati da un grado di generalità tale da non determinare restrizioni a priori sulle caratteristiche della tecnologia, consentendo dunque la maggiore “libertà di espressione” ai dati in nostro possesso.
Non è certamente questa la sede per una rassegna metodologica ed un’analisi approfondita dei pregi e dei difetti dei due approcci (si veda a questo proposito Mundlak, 2001 e Just e Pope, 2001). Di seguito vogliamo soltanto indicare come l’approccio attraverso i modelli econometrici consenta di produrre informazioni variegate di grande valore per l’analisi delle politiche agricole e la simulazione degli interventi, in grado di fornire elementi di valutazione ai policy maker. A questo proposito, di seguito illustriamo alcune delle numerose applicazioni,che fanno riferimento al nostro paese e ad alcune delle problematiche più dibattute che negli ultimi anni hanno interessato il settore agricolo.
Caso 1 - Modellare l’impatto della riforma della politica agricola: il caso dei seminativi
La riforma Mac Sharry del 1992 ha posto il problema di modellare l’impatto degli aiuti diretti sull’offerta dei seminativi COP (Cereali, Oleaginose e Proteaginose) e di valutarne il grado di disaccoppiamento. Un possibile approccio econometrico consiste nell’estendere il modello standard della funzione di profitto per tener conto dell’allocazione della terra tra le diverse destinazioni (colture e/o set-aside), visto che il regime di pagamenti in vigore fino al 2005 prevedeva l’erogazione di aiuti legati alle superfici investite e alle superfici eventualmente destinate a set-aside obbligatorio.
Pur essendo possibile applicare questo modello a dati aggregati (cioè serie storiche aggregate, di norma annuali), in realtà appare molto più logico stimarlo su dati aziendali, come quelli dell’indagine RICA (Rete d’Informazione Contabile Agricola). Per lo specifico caso della PAC-seminativi, l’uso dei dati aziendali è preferibile perché, per come sono stati applicati gli aiuti diretti, nei fatti si è realizzata un’estrema differenziazione del livello di questi aiuti tra aree territoriali (si pensi alla frammentazione del piano di regionalizzazione applicato in Italia).
Partendo dunque da una funzione di profitto estesa per includere gli effetti degli aiuti, si possono ricavare e stimare simultaneamente le equazioni di offerta delle principali colture, di domanda degli input variabili e di allocazione della terra alle stesse colture (Moro e Sckokai 1999).
Per questo tipo di analisi, il risultato chiave in termini di simulazione dell’impatto della PAC è l’elasticità rispetto agli aiuti diretti, un dato che può essere utilizzato come input per altri modelli che effettuano simulazioni su larga scala.
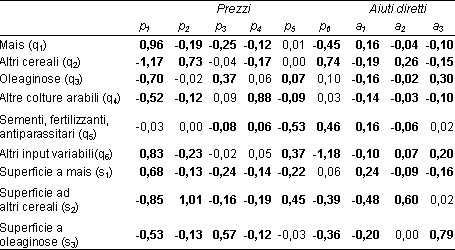
A titolo di esempio, in Tabella 1 si forniscono i risultati del lavoro di Moro e Sckokai (1999), dove si vede chiaramente come l’offerta delle diverse colture COP risponda in modo positivo ai pagamenti per ettaro, a dimostrazione di come questi ultimi abbiano influito significativamente sulle quantità prodotte e non possano quindi essere classificati come “disaccoppiati”. Questo impatto è però decisamente più forte sulle superfici investite che non sulle quantità offerte, in quanto le elasticità delle prime rispetto agli aiuti sono sistematicamente più alte delle corrispondenti elasticità delle equazioni d’offerta. Questo implica che il carattere parzialmente disaccoppiato degli aiuti diretti abbia influenzato maggiormente le superfici investite, spingendo gli agricoltori ad adottare tecniche tendenzialmente meno intensive, in linea con gli obiettivi di maggiore compatibilità ambientale dell’attività agricola introdotti dalle recenti riforme della PAC.
Il modello in questione, come in generale i modelli analoghi, può essere ulteriormente ampliato per tener conto degli effetti del rischio sulle decisioni degli imprenditori (Sckokai e Moro, 2006); i risultati prodotti sono qualitativamente simili a quelli appena illustrati, ma incorporano anche gli effetti di una variabile cruciale per le attività agricole come il rischio di prezzo.
Tabella 1 - Stime delle elasticità dell’offerta ai prezzi p e agli aiuti a, su dati RICA 1993-95
Caso 2 - Programmare e simulare politiche alternative e scenari futuri: rendita e quote latte
Con la riforma delle PAC del 2003, il regime delle quote di produzione del latte è stato esteso fino alla campagna 2014-15; ciò non ha però interrotto il dibattito sulle prospettive di riforma dell’Organizzazione Comune di Mercato (OCM) del latte, in cui rimane forte la posizione di coloro che prefigurano l’eliminazione delle quote a partire dal 2015. In questo senso, quindi, cresce la domanda di studi che siano in grado di simulare adeguatamente l’impatto di uno scenario così radicale. È ben noto che la presenza di un regime di controllo dell’offerta, combinato con meccanismi di sostegno del prezzo, crea un “gap”, la cosiddetta “rendita della quota”, tra il prezzo di vendita e il costo marginale di produzione, che invece, in condizioni concorrenziali e in assenza di interventi, dovrebbero eguagliarsi. La stima di questa rendita è un elemento chiave per poter simulare l’impatto di scenari alternativi, in particolare nel caso si ipotizzi la rimozione delle quote.
Per stimare il valore medio di questa rendita, è possibile procedere attraverso la stima di una funzione di costo di medio-lungo periodo. In Moro, Nardella e Sckokai (2005), le rendite derivanti dalle quote sono state stimate per i paesi UE-15 (Tabella 2), utilizzando una funzione di costo che produce le classiche curve di costo medio/marginale a forma di U. Anche in questo caso la stima è stata condotta sui dati aziendali dell’indagine RICA.
I risultati mettono in evidenza le forti differenze nella struttura dei costi aziendali esistenti tra i diversi paesi UE-15, differenze che porterebbero ad un impatto molto diverso della rimozione delle quote. Ad esempio, nei grandi paesi produttori di latte (Italia, Germania, Francia, Regno Unito) una quota molto significativa di aziende si colloca nel tratto decrescente della curva di costo marginale, una situazione di evidente inefficienza, provocata molto probabilmente dal permanere della quota di produzione, che ha impedito alle aziende di adeguarsi all’evolvere della tecnologia, e dalla contemporanea presenza di un prezzo del latte artificialmente sostenuto. In caso di rimozione delle quote, la permanenza sul mercato di queste aziende potrebbe essere messa a rischio da un prezzo del latte che dovesse scendere eccessivamente.
Tabella 2 - Stima delle rendite derivanti dalle quote latte nei paesi UE-15*
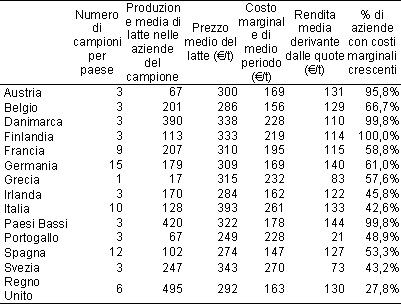
*Costi marginali calcolati come media ponderata dei costi marginali di ciascuna azienda, utilizzando come pesi la rappresentatività di ciascuna azienda nel campione RICA
Caso 3 - Modelli di equilibrio parziale e competizione imperfetta
La maggior parte dei modelli utilizzati in ambito agricolo per fare previsioni e/o simulazioni di interventi si basa sull’ipotesi di mercati perfettamente competitivi. Il moderno sistema agroalimentare si caratterizza invece per una progressiva riduzione dei rapporti di mercato, sostituite da varie forme contrattuali, e soprattutto per l’esistenza di forme di competizione imperfetta nei rapporti di filiera, che coinvolgono sia la produzione agricola che il consumatore finale.
Gli economisti agrari hanno pertanto iniziato a tenere conto nei propri modelli dell’esistenza di strutture di competizione imperfetta (oligopolistiche e oligopsonistiche) nelle filiere agroalimentari, in modo da evitare che le indicazioni fornite dai modelli di previsione e/o simulazione ne vengano eccessivamente distorte.
Il potere di mercato può essere introdotto nei modelli di mercato e/o di settore in ambito agricolo attraverso la specificazione di elementi di competizione imperfetta nelle equazioni di trasmissione dei prezzi:

per cui il prezzo finale del prodotto trasformato, PC, ed il prezzo della materia prima agricola, PP, aggiustata per un coefficiente di conversione c, sono legati dai costi di trasformazione M e dall’influenza di un possibile elemento oligopsonistico da parte degli acquirenti/trasformatori delle materie prime agricole (l’elasticità congetturale ECP relativa ai mercati alla produzione, la cui elasticità dell’offerta è data da eP) e di un possibile elemento oligopolistico da parte soprattutto delle grandi catene distributive (l’elasticità congetturale relativa ai mercati al consumo, la cui elasticità di domanda è data da eC).
Punto cruciale è la determinazione dell’entità del potere di mercato, rappresentato sostanzialmente dal valore delle elasticità congetturali ECC e ECP; quanto più queste elasticità sono diverse da zero, tanto maggiore le filiere in esame si discostano da un regime di concorrenza perfetta. Seppure queste elasticità, sotto opportune restrizioni, possano essere approssimate da misure di concentrazione del settore, è possibile utilizzare l’analisi econometrica per ottenere stime di questi parametri.
Ad esempio, il settore lattiero-caseario in Italia è stato modellato con un modello di equilibrio parziale (Moro, Sckokai e Soregaroli, 2006) che include gli effetti del potere di mercato. La trasformazione delle materie prime avviene lungo filiere non perfettamente competitive, sia tra gli acquirenti/trasformatori, dove però il prezzo di sostegno interviene a mitigarne l’impatto, che tra le catene distributive. Per misurare il potere di mercato a livello dei mercati finali si è proceduto alla stima simultanea di equazioni di domanda e di trasmissione dei prezzi per i principali prodotti della trasformazione del latte, in modo da ottenere valori approssimati delle elasticità congetturali, come riportato in Tabella 3.
Tabella 3 - Stima del potere di mercato ECC nel settore lattiero caseario in Italia

*Significatività al 95%
Come si vede, la presenza di potere di mercato è comprovata dalla significatività dei parametri stimati, ed è particolarmente elevato per il latte alimentare e gli altri prodotti lattiero-caseari. Di conseguenza, i riflessi sulle performance dei modelli di previsione/simulazione possono essere anche rilevanti: in Tabella 4 si riportano le differenze nelle principali variabili di mercato di un esercizio di simulazione degli effetti della riforma Fischler sul settore lattiero-caseario italiano per un orizzonte di breve-medio termine.
Come si può vedere, le previsioni sui livelli dei prezzi alla produzione e soprattutto al consumo sono diverse; il non tenere conto della presenza di potere di mercato lungo la filiera della trasformazione lattiero-casearia porta a sovrastimare, alla fine dell’orizzonte temporale di simulazione, l’impatto sui prezzi al consumo di formaggi DOP e di latte alimentare, mentre sottostima quello su prezzi al consumo del burro ed altri derivati lattiero-caseari. A livello agricolo, la presenza di potere di mercato riduce invece i prezzi della materia prima di un ulteriore 1% rispetto allo scenario di competizione perfetta.
Tabella 4 - Differenze percentuali nei livelli dei prezzi di mercato Simulazione dell’impatto della riforma Fischler sul settore Lattiero- caseario in Italia

Riferimenti bibliografici
- Moro D., Nardella M., Sckokai P. (2005), "Regional distribution of short-run, medium-run and long-run quota rents across EU-15 milk producers", Contributed paper” all’XI Congresso della European Association of Agricultural Economists (Copenhagen, 23-27 agosto, 2005)
- Moro D., Sckokai P. (1999), "Modelling the CAP arable crop regime in Italy: Degree of decoupling and impact of Agenda 2000", Cahiers d’Economie et Sociologie Rurales, n. 53, pp. 49-73
- Moro D., Sckokai P., Soregaroli, C. (2006), "Dairy policy modelling under imperfect competition", Contributed paper al XXV Congresso della International Association of Agricultural Economists (Brisbane, Australia, 13-18 agosto, 2006)
- Mundlak Y., (2001), "Production and supply", in Gardner B.L., Rausser G.C., (a cura di), Handbook of Agricultural Economics – Volume 1, North-Holland, Amsterdam, pp. 3-85
- Just R.E, Pope R.D. Mundlak Y., (2001), "The agricultural producer: Theory and Statistical measurement", in Gardner B.L., Rausser G.C., (a cura di), Handbook of Agricultural Economics – Volume 1, North-Holland, Amsterdam, pp. 3-85
- Sckokai P., Moro D. (2006), "Modeling the Reforms of the Common Agricultural Policy for Arable Crops under Uncertainty", American Journal of Agricultural Economics, vol. 88, n. 1, pp. 43-56

